Grundlagen Audio
Begriffe
Ein Ton ist eine Schwingung, die durch periodische Regelmäßigkeit eine definierbare Grundfrequenz – die Tonhöhe – hörbar werden läßt. Der Klang eines Tons hängt von den Anteilen weiterer Schwingungen innerhalb der Grundschwingung ab. Ein Geräusch – etwa einer Rassel – hat dagegen keine periodische Grundschwingung, die Luftdruckschwankungen verlaufen so unregelmäßig, daß keine Tonhöhe definierbar ist. Die Übergänge zwischen Ton und Geräusch sind fließend, denkt man daran, daß sich Konzertpauken sehr wohl stimmen lassen, obwohl sie als perkussive Instrumente bereits sehr diffuse Klangspektren erzeugen.
Sound wird heute oft im ›Multimedia-Deutsch‹ für alles, was mit dem Audiobereich zu tun hat verwendet. Zum Teil geschieht das sicher aus Unkenntnis der Begriffe aus Akustik und Musik. Der Begriff Sound hat jedoch auch Vorteile, da er problematische Fragen der traditionellen Begriffe und Wissenschaftsdisziplinen ausblendet (Was ist Musik?!).
Sprache ist danach ein geräuschhaftes, d.h. ein nichtperiodisches Klangereignis, das durch seine definierten Frequenzgemische sprachliche Lautmuster enthält. Im Gesang werden diese Lautmuster einer periodischen Schwingung aufmoduliert.
Für gute Sprachverständlichkeit reicht ein Frequenzbereich bis 8 kHz vollkommen aus.
Beispiele für Schwingungen im Audiobereich
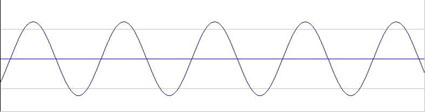
Sinuswelle – Die einfachste Form einer periodischen Schwingung, sie besitzt keine weiteren Frequenzanteile
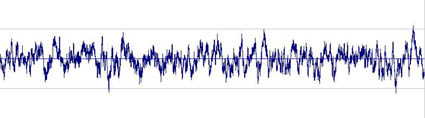
Rauschen – ›Schwingungschaos‹, das Gegenteil einer periodischen Schwingung
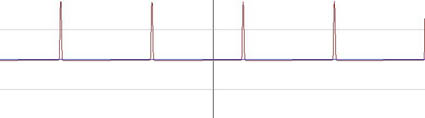
Obertonreiche Schwingung – hier als Beispiel eine pulsbreitenmodulierte Sägezahnschwingung, also ein Sägezahn, dessen Anlaufflanke verschoben und verkürzt wurde

Perkussiver Klang – hier als Beispiel ein metallisch klingender Synthesizerklang, dessen Tonhöhe noch deutlich wahrzunehmen ist. Eine weitere Erhöhung der Komplexität des Frequenzgemischs würde den Ton in ein Geräusch übergehen lassen.
Klang – Analyse und Synthese
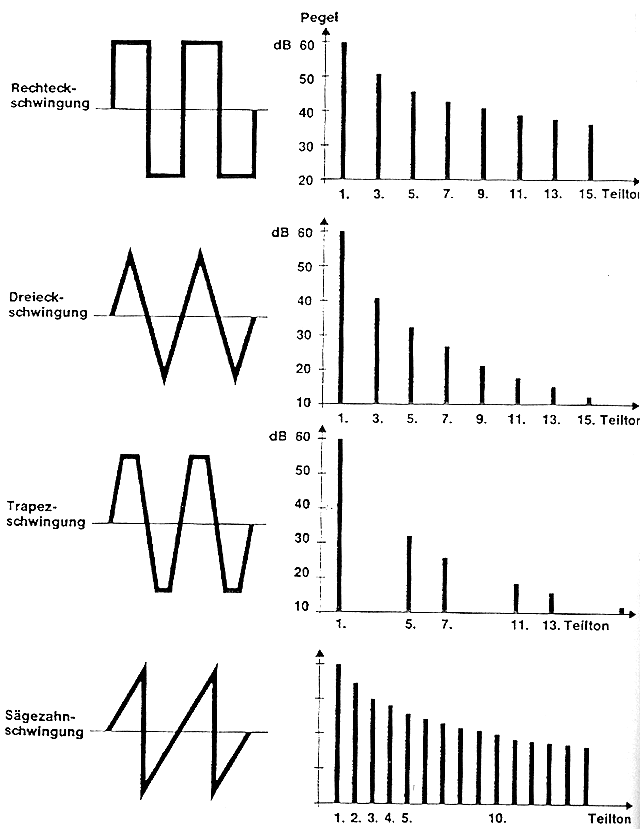
›Klangfarben‹ sind Frequenzgemische, deren Obertonstruktur nicht den Eindruck eines Mehrklangs hervorruft – also das gleichzeitige Erklingen noch unterscheidbarer Einzeltöne –, sondern den spezifischen Klangeindruck eines Tons oder Geräuschs ausmacht. Künstlich erzeugte Standard-Wellenformen (durch Synthesizer-Hard- oder Software) haben beispielsweise folgende Obertonanteile:
Fourieranalyse
»Der Satz von Fourier besagt zusammenfassend, dass man jede periodische Schwingung, wie kompliziert sie auch sein mag, als die Überlagerung reiner, harmonischer Schwingungen darstellen kann, deren Grundfrequenz durch die Wiederholfrequenz der periodischen Schwingung gegeben ist.« (Ackermann, S. 16)
Im praktischen Umgang mit Audiosignalen ist die davon abgeleitete Fast Fourier Transformation (FFT) von Bedeutung, mit welcher der spektrale Aufbau (Amplitudenspektrum) des zu analysierenden Audiosignals berechnet werden kann.
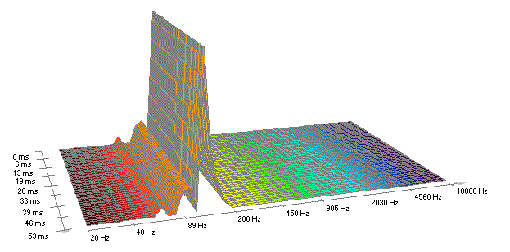
FFT-Darstellung einer Sinus-Welle
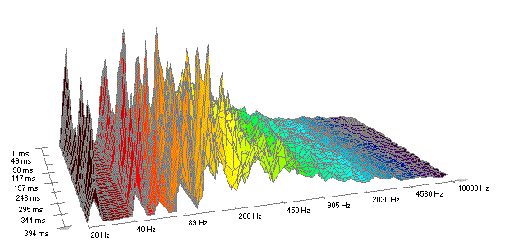
FFT-Darstellung eines Rausch-Signals
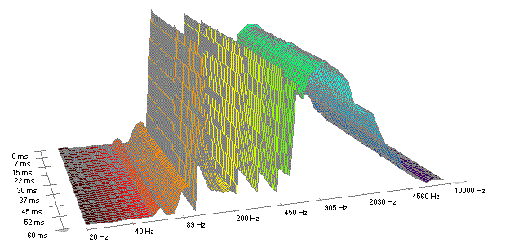
FFT-Darstellung einer pulsbreitenmodulierten Sägezahn-Schwingung
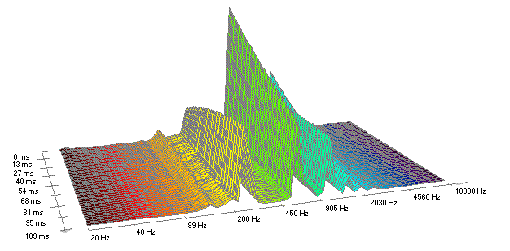
FFT-Darstellung eines permissiven Klangs
Naturinstrumente erzeugen typische Frequenzspektren durch ihre physischen Resonanzen. Hier bspw. die Erzeugung von Freuquenzanteilen bei einer Geige:
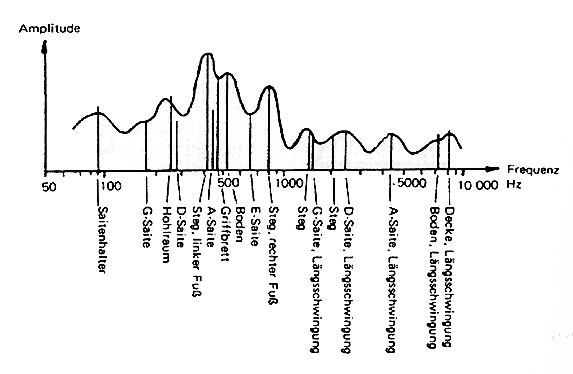
Hüllkurve
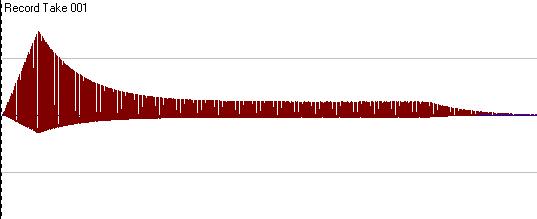
›Hüllkurve‹ nennt man den Zeitverlauf zentraler Parameter innerhalb eines Tons oder Geräuschs. Die wichtigsten Parameter sind bei elektronisch erzeugten bzw. bearbeiteten Sounds die Amplitude (Lautstärke) und Filtereinstellungen.

Audio-Daten vs. MIDI-Daten
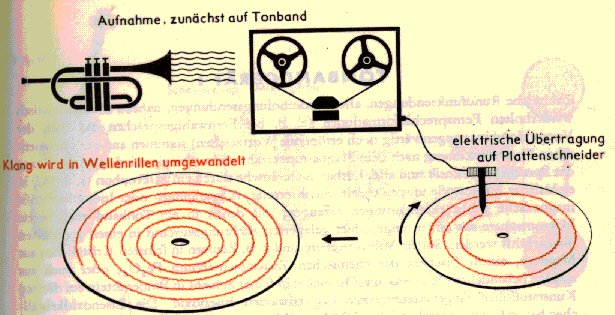
Audiodaten bilden Luftdruckschwankungen ab. Da diese zunächst in elektrische Spannungsschwankungen umgesetzt werden, codieren sie präzise gesagt einen elektrischen Spannungsverlauf in den Parametern Amplitude/Zeit.
Damit Audiodaten aufgenommen und wiedergegeben werden können, werden A(nalog)/D(igital)-Wandler bzw. D/A-Wandler benötigt. Am A/D-Wandler wird aus der kontinuierlichen Spannungsschwankung eine (zeit-)diskrete Folge diskreter Werte. Am D/A-Wandler wird aus einer solchen Folge wiederum ein kontinuierlicher Spannungsverlauf (re)konstruiert.
Hier zeigt sich der ›klassische Abbildungsaspekt‹ phonographischer Medien. D.h. ein Verständnis eines Mediums (im Sinne von Über- bzw. Vermittlung): als ›Abbildung‹ eines Phänomens auf einen Träger und als dessen Re-Produktion. Shannon/Weavers Modell der Signalübertragung verdeutlicht diesen Aspekt:
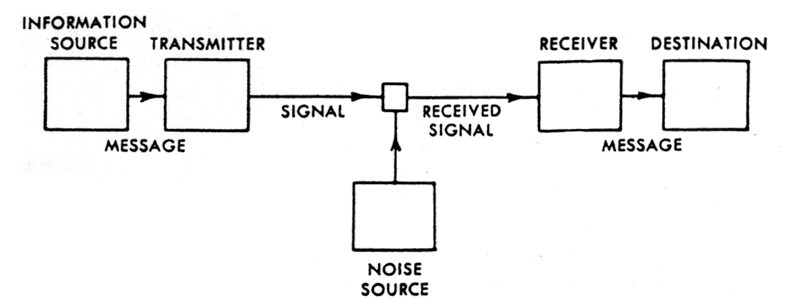
Intermedial ist dieses Medienverständnis vergleichbar mit der Pixelorientierung bei Bildmedien (Fotografie, Bitmap), oder der Abbildungen von Schrift bei Textmedien (Kopierer, FAX). Spezifische Fehler sind solche, die die ›Abbildungs‹-Qualität beeinträchtigen: Knackser, Rauschen, Dynamikprobleme.
MIDI-Daten sind wiederum Steuerungsdaten. Es handelt sich um (technische) Anweisungen zur Generierung von Klängen (ähnlich wie traditionelle Notation). Um MIDI-Daten zum Klingen zu bringen, wird ein entsprechender Klangerzeuger (Synthesizer) benötigt.
Der generativer Aspekt des Mediums tritt hier in den Vordergrund, sein ›Instrumentcharakter‹ im musikalischen Sinne. Es handelt sich um einen automatischen Generator; statt Abbildung/Übertragung steht ein generatives Moment im Vordergrund. Erst ein neueres Medienverständnis zählt solche generativen Aspekte zu den Eigenschaften aller Medien und gewichtet das Verhältnis von Abbildung und Produktion neu.
Intermedial vergleichbar ist dieses Medienverständnis mit der Objektorientierung (Zerlegung in geometrische Grundformen; Vektorgrafik) bei Bildmedien oder auch der digitalen Codierung des Alphabets bei Textmedien (ASCII; Word Processing). Spezifische Probleme sind solche einer hörbaren ›Technizität‹ der generierten Struktur: etwa mechanischer Rhythmus und Klang, Totalaussetzer.
Diese Trennung zwischen zwischen abbildendem und generativen Aspekt auditiver Medien ist immer nur eine analytische. In konkreten technischen Setups greifen beide Aspekte oft ineinander. Als frühe Zwischenformen lassen sich zum Beispiel mechanische Musikautomaten betrachten. Hier wird eine bestehende musikalische Struktur abgebildet, allerdings wird sie eben nicht phonographisch, d.h. als klingendes Ereignis mitgeschrieben. Es werden also keine Luftdruckschwankungen medial codiert, sondern die musikalische Struktur umcodiert, z.B. von der Partitur auf eine Stiftwalze. Diese Walze übernimmt dann, wie der MIDI-Code, die technische Steuerung einer Klangerzeugung, die das Stück wieder hörbar werden lässt.
Digital Audio
Analoge Audiosignale sind kontinuierliche Signale. Bei der Digitalisierung werden diese in eine regelmäßige Folge von diskreten Werten gewandelt. Hierzu wird die Amplitude des Signals in regelmäßigen Abständen abgetastet und den einzelnen Stichproben (Samples) Werte aus einer begrenzten Wertemenge zugeordnet (Quantisierung). Dabei wird ein Raster verwendet, dass die möglichen Werte bestimmt. Die Abtastfrequenz (Abtastrate, Abtastfrequenz, Samplefrequenz, Samplerate; in Hz oder kHz angegeben) bestimmt, wie oft das Signal pro Sekunde abgetastet wird. Die Auflösung (Quantisierung; in bit angegeben) legt die mögliche Wertemenge pro Sample fest.
Die Digitalisierung von Audiodaten erfordert eine A/D- (und natürlich am Ende des Prozesses eine D/A) Wandlung. Der weit verbreitete sogenannte ›CD-Standard‹ für die Audiohardware ist eine Digitalisierung in ›Zeitscheiben‹ von 44,1 kHz und einer ›Lautstärkerasterung‹ von 16 bit.

Jeder dieser Balken visualisiert einen diskreten Meßwert (ein Sample in der technischen Definition). Die gezackte Begrenzungslinie entspricht in Annäherung dem kontinuierlichen Verlauf der Welle.
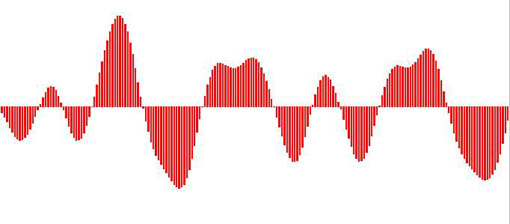
Dieses Verfahren heißt in der Fachsprache Pulse-Code-Modulation (PCM). In der Praxis wird statt der jeweiligen Abtastwerte oft nur die Differenz zur letzten Messung (Differential PCM), oder die Richtung des nächsten Werts (Delta-Modulation, 1-bit Wandlung) bestimmt, bevor zum Standard-Datenformat transformiert wird.
Datenübertragung und Speicherung
für Audiodaten richtet sich nach den allgemeinen Möglichkeiten für Speicherung auf Festplatten, Wechselmedien etc. und Netzübertragung (Internet, LAN etc.). Dabei sind Hardware (Speicher- und Übertragungskapazität) und Software (Cacheorganisation und Protokolle) zu berücksichtigen. Sind Audiodaten erst einmal digitalisiert, unterscheiden sie sich um nichts von Text- oder Bild-Daten.
Die Datenrate, die dabei pro Sekunde und Kanal anfällt, entspricht der Sampleauflösung mal der Samplefrequenz.
Beim üblichen Format (CD-Standard): Stereo, 44,1 kHz, 16 Bit ergeben sich:
2 (für 2 Stereokanäle) x 44100 x 16 = 1.411.200 Bit/s oder 176.400 Byte/s oder 172,26 KByte/s.
Übertragungsraten
| 44,1 kHz | 22 kHz | 11 kHz | |
| 16 Bit | 172 KByte/s | 88 KByte/s | 44 KByte/s |
| 12 Bit | 132 KByte/s | 66 KByte/s | 33 KByte/s |
| 8 Bit | 88 KByte/s | 44 KByte/s | 22 KByte/s |
Übertragungsraten (komprimiert):
Typische Performance Daten von MPEG-1 Layer III (MP3)
| sound quality | bandwidth | mode | bitrate | reduction ratio |
| „telephone sound“ | 2.5 kHz | mono | 8 Kbps | 96:1 |
| „better than shortwave“ | 4.5 kHz | mono | 4.5 kHz | 48:1 |
| „better than AM radio“ | 7.5 kHz | mono | 32 Kbps | 24:1 |
| „similar to FM radio“ | 11 kHz | stereo | 56…64 Kbps | 26…24:1 |
| „near CD“ | 15 kHz | stereo | 96 Kbps | 16:1 |
| „CD“ | 15 kHz | stereo | 112..128 Kbps | 14..12:1 |
Faustregeln für den Bedarf an Speicherplatz: Pro Minute werden bei unkomprimierten Daten (Stereo, 44,1 kHz, 16 bit) ca. 10 MByte Speicherplatz benötigt, bei stark komprimierten Daten (Real Audio, MPEG-1/Layer 3) ca. 1 MByte.
Spitzfindigkeiten mit bits und Bytes:
1 Byte = 8 bit (ein halbes ‚Datenwort‘ von 16 bit);
1 kbit = 1000 bit
Die Präfixe Kilo (K) und Mega (M), die im Normalgebrauch den Faktor 1.000 bzw. 1.000.000 bezeichnen, werden im Bereich der bits und Bytes oft nach den 2er-Potenzen des binären Systems verwendet, also:
1 Kbit = 1024 bit = 128 Byte
1 Mbit = 1024×1024 bit = 1048576 bit = 131072 Byte = 128 KByte
Diese Praxis wurde allerdings offiziell seit 1996 geändert und folgende Benennung vorgeschlagen: 1 Kibibyte (KiB) = 1024 Byte, 1 Mebibyte (MiB) = 1024 · 1024 Byte. Dennoch existieren bis heute verschiedene Verwendungen nebeneinander, so dass Verwirrungen möglich sind: Eine nach dem dezimalen 1 TByte angegebene Festplatte wird etwa vom Betriebssystem im binären Kontext mit 931 GByte erkannt.
Audiodatenformate
Unkomprimierte Formate:
.wav (MS-Windows-Format)
.aiff (audio interchange file format; auf Apple-Plattformen üblich)
Komprimierte Formate / Internet:
* MP3 (=MPEG 1; Layer 3) als gängigstes DRM-freies Dateiformat; Dateiendung .mp3
MP3 erlaubt als Kompressionscodec keine erweiterten Funktionen, selbst die bekannten ID3-Tags mit Angabe von Artist, Title etc. sind nur durch einen Trick möglich. Allerdings können die Dateien – wie jede andere Datei auch – mit einem Watermark (z.B. beim Kauf) ‚gestempelt‘ werden
* MP4 (=Container mit oder ohne DRM + meistens MP3 oder AAC codierten Daten) als neueres praktisches Containerformat mit hochwertig und effizient codierten Inhalten; Dateiendungen .mp4, .m4a (audio), .m4p (protected audio)
Beispiel: Audiodateien aus dem iTunes-Shop bestehen aus einem MP4 Container mit Apples DRM FairPlay und AAC codierten Inhalten
* WMA (=Microsofts proprietäres Audiokompressionsformat mit integrierter DRM Funktionalität); Dateiendungen .wma, .asf (advanced streaming format=streaming container für wma und anders codierte Daten)
WMA ist eng an das Windows-Betriebssystem gebunden, inzwischen erlauben jedoch auch Programme wie iTunes die Konvertierung von nicht DRM beschränkten WMAs in andere Formate
* AAC (Advanced Audio Coding) ist ein verbessertes MPEG 2 Verfahren.
Aussteuerung
Eine möglichst gute Aussteuerung des Aufnahmepegels ist die Voraussetzung für eine rauscharme und dynamikreiche A/D Wandlung. Anders als bei analogen Aufnahmeverfahren, für die diese Regel ebenfalls gilt, gibt es allerdings bei der Digitalisierung keinen Grenzbereich, sondern eine genau definierte obere Pegelgrenze, bei deren Überschreiten keine Abbildung der Wellenform mehr möglich ist. Es wird solange nur ein Wert (der Höchstwert) gemessen, wie der zulässige Pegel überschritten wird. Resultat ist eine ‚gekappte‘ Welle, die sich einer Rechteckschwingung annähert und mit dem Original kaum noch etwas gemeinsam hat.
Interferenz
Überlagerung zweier oder mehrerer Schwingungen mit dem Ergebnis von Interferenzschwingungen (Schwebungen)
Die Digitalisierung kontinuierlicher Phänomene wie Bilder und Töne ist prinzipiell mit einer Rasterung verbunden. Dabei können sich die Rasterfrequenz und eine wellenförmige Struktur des Gegenstands überlagern und weitere, vorher nicht existente Schwingungen ergeben. Interferenzprobleme bei der Digitalisierung treten aus zwei Ursachen auf:
– das zu digitalisierende Phänomen hat selbst eine ›natürliche‹ Wellenstruktur, wie etwa die Luftschwingungen des Schalls oder sich periodisch bewegende Gegenstände im Bewegtbild oder
– ein ›naturgemäß‹ unperiodisches Phänomen wurde durch Medientransformationen bereits gerastert.
Aliasing
Beim Digitalisieren können Frequenzen entstehen, die im Original nicht vorhanden sind. Diese Artefakte oder ›Aliasfrequenzen‹ des Digitalisierungsvorgangs sind Ergebnisse einer unzureichenden Abtastfrequenz. Auch hier gilt – wie bei jedem Wellenphänomen und beim Bild bereits besprochen – das Nyquist/Shannon-Theorem: Die Abtastrate muß mindestens das Doppelte der zu digitalisierenden Frequenz betragen.
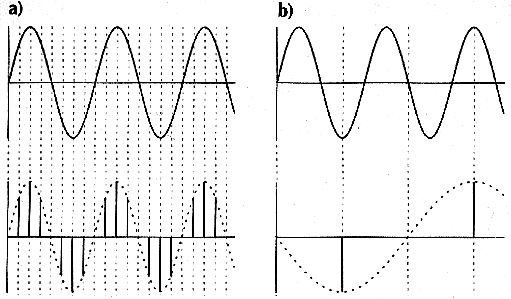
Da in Audiosignalen immer – ob gewünscht oder nicht – hochfrequente Anteile vorhanden sind, die jede Datenrate und Speicherkapazität sprengen würden, gibt es nur zwei Lösungswege für dieses Problem (i.d.R. kombiniert angewandt):
Filterung – im Audiosignal werden alle Frequenzen über der beabsichtigten halben Digitalisierungsfrequenz herausgefiltert. Es ist allerdings mit vertretbarem Aufwand nicht möglich, auf analogem Wege alle Frequenzen zu entfernen, sie werden lediglich gedämpft (›Q-Faktor‹, ›Dämpfungsfaktor‹, ›Flankensteilheit‹ des Filters).
Oversampling – das Signal wird mit einem Vielfachen (z.B. 64fach) der Abtastfrequenz abgetastet, um Aliasing zu vermeiden. Auf digitalem Weg werden dann die hohen Frequenzen herausgerechnet. Oft wird die Kombination beider Verfahren angewendet.
Die folgenden Beispiele zeigen die Verteilung der einzelnen Meßpunkte in Abhängigkeit von der Freqenz der zu digitalisierenden Schwingung. Die Samplingfrequenz beträgt bei allen Beispielen 44100 Hz.
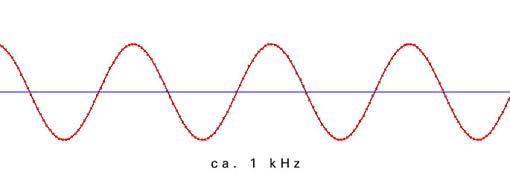
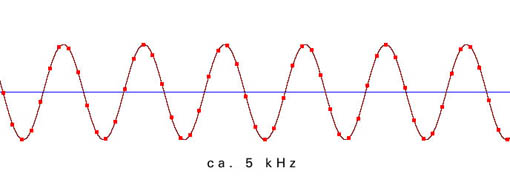
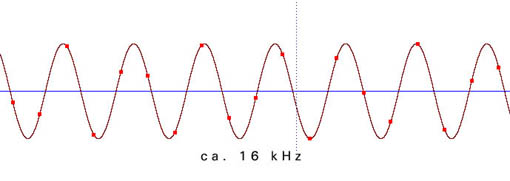
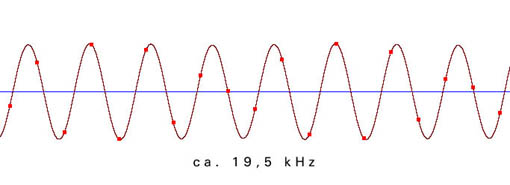
Aus der ungenauen Abtastung in der Nähe der Grenzfrequenz ergibt sich ein phasenungenaues und amplitudenverändertes Signal:
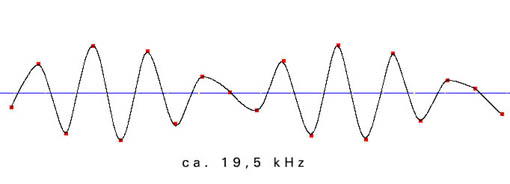
Dynamik – Signal/Rauschabstand
Die Dynamik eines Signals bezeichnet den Umfang seiner Lautstärkeunterschiede oder einfacher gesagt, sie bestimmt, wie weit sich ein Pianissimo und ein Fortissimo unterscheiden. Um die Nuancen eines Konzerts für Violine und Orchester wiederzugeben, ist eine wesentlich größere Dynamik erforderlich als etwa für eine Nachrichtensendung. Manchmal ist eine große Dynamik sogar unerwünscht, etwa in Werbeclips, die sich durch einen gleichbleibend hohen Pegel aus dem Programmumfeld herausheben sollen.Gemäß den Eigenschaften des menschlichen Gehörs wird die Dynamik in der logarithmischen Einheit Dezibel angegeben.
| Sprache | Sologesang | Streicher | Klavier | Orchester |
| 15-20 dB | 40-50 dB | 30-35 dB | 40-50 dB | 30-70 dB |
Um die Dynamik des Originalsignals beizubehalten, muß der Signal/Rauschabstand der Dynamik des Originalsignals mindestens entsprechen. Bei elektrischen und elektronischen Übertragungssystemen wird die technisch mögliche Dynamik als Systemdynamik bezeichnet. Sie ist als Differenz von Übersteuerungsgrenze und Rauschpegel definiert.
| Studioverstärker | Plattenspieler | Compakt Cassette | MW-Radio | Muzak Tape |
| 100 dB | 50 dB | 40 dB | 30 dB | 20 dB |
Die maximale Systemdynamik digitaler Systeme errechnet sich nach der Formel:
S(ignal)/N(oise) [dB] = 6,02n + 1,76
n entspricht der Länge der Binärzahl in Bit. Bei einer Auflösung von 16 Bit beträgt die maximale Systemdynamik demnach ca. 98 dB. Die tatsächlich nutzbare Dynamik und somit der effektive Signal/Rauschabstand liegt allerdings weit darunter, da ein bewerteter Störpegel von 14 dB, ein Schutzabstand zum Störpegel von 20 dB (Footroom) und eine Aussteuerungsreserve von 10 dB (Headroom) berücksichtigt werden müssen. Bei einer 16-Bit-Auflösung ergibt sich somit ein effektiver Signal/Rauschabstand von 54 dB. Dynamik [dB] = 98 – 14 – 20 -10 = 54
Quantisierungsfehler
Da das wertkontinuierliche Analogsignal bei der Digitalisierung auf Werte einer endlichen Wertemenge abgebildet wird, kommt es zu Rundungsfehlern. Da diese Fehlerbeträge im Zeitverlauf statistisch gleich verteilt auftreten, können sie als Rauschen interpretiert werden (Quantisierungsrauschen). Insbesondere bei Signalen, die in einem geradzahligen Verhältnis zur Abtastfrequenz stehen, ergibt sich ein unangenehmes ‚tonales‘ Rauschen, da die Fehlerrate nicht mehr zufällig ist, sondern dem Phasenverhalten des Signals folgt.

Dithering
Um den signalabhängigen Klangcharakter des Quantisierungsrauschens bei geringer Aussteuerung des abzutastenden Signals zu unterdrücken, wird dem Originalsignal vor der Digitalisierung eine geringe Rauschspannung (Dither-Rauschen) beigemischt. Auch bei der Requantisierung auf digitaler Ebene wird ein Dithersignal zugesetzt, um die dabei entstehenden Fehler zu maskieren.
Grundfunktionen der Audiobearbeitung (Sample-Editing)
Je nach Ziel der Bearbeitung, etwa Aufbereitung einer Audiodatei für eine Multimedia-Anwendung oder musikalische Gestaltung von ‚Rohmaterial‘, können verschiedene Abfolgen von Arbeitsschritten sinnvoll sein. Dennoch soll die Reihenfolge der hier genannten Verfahren eine Orientierung für die Folge in der Praxis geben.
Normalisieren
Die Pegel jedes Meßpunktes werden gleichmäßig soweit angehoben, bis die höchsten Pegel den voreingestellten Maximalwert erreichen. Damit wird zwar prinzipiell keine Dynamik gewonnen, jedoch Rauschen und Klangprobleme durch die bessere Ansteuerung von Peripheriegeräten vermieden.
Normalisieren ist außerdem für viele weitere Rechenschritte mit digitalisiertem Material günstig, da Rundungsfehler bei Rechenoperationen mit größeren Werten weniger ins Gewicht fallen.
Nach pegelverändernden Operationen kann erneutes Normalisieren sehr sinnvoll sein.
Cut, Copy and Paste
Wie aus der Text- und Bildbearbeitung bekannt, kann im Wave-Editor Audiomaterial geschnitten werden:
Cut: Ausschneiden
Copy: Kopieren in die Zwischenablage
Paste: Einfügen der Daten aus der Zwischenablage
Trim/Crop: Freistellen des ausgewählten Bereichs
Es sollte darauf geachtet werden, immer in den Nulldurchgängen zu schneiden, so daß keine Knackser entstehen. Bei Stereosignalen kann die Suche nach einem gemeinsamen Nulldurchgang beider Signale ein wenig kniffelig sein…
Loops
Durch Wiederholen eines bestimmten Segments (oder auch des gesamten Materials) entsteht ein Loop. Dieser kann z.B. dazu benutzt werden, die quasistationäre (Sustain-)Phase eines Klanges zu verlängern oder um eine ständige Rhythmusspur (Drumloop) zu erzeugen. Bei Multimedia-Anwendungen kann so Speicherplatz gespart und die Performance verbessert werden.
Filter / Equalizer
sind sowohl für die ästhetische Gestaltung wie auch für die einfache Aufbereitung von Daten wichtig. So kann etwa die Sprachverständlichkeit vor einem Resampling verbessert werden, oder es können störende Resonanzen des Aufnahmeraums oder der Mikrophonierung beseitigt werden.
Kompressor / Limiter
Der Kompressor macht – einfach gesagt – ein lautes Signal leiser und ein leises Signal lauter. Die Dynamik eines Signalverlaufs wird so ‚zusammengedrückt‘. Für Anwendungen mit niedrigerer Dynamik als die der Originalaufnahme bieten sich Kompressoren an, um das Feld der dynamischen Bandbreite zu kontrollieren. Auch vor der Verminderung der Bitrate (z.B. 16 bit nach 8 bit für Multimedia- oder für Internetanwendungen kann durch gezielte Kompression Klangqualität ‚gerettet‘ werden.
Die ‚Lautheit‘ eines Signals in einem Umfeld läßt sich ebenfalls mit Kompressoren steuern. Stark komprimierte Signale können einen gleichbleibend hohen Pegel erhalten und heben sich so aus einem normalen dynamischen Umfeld heraus (>Werbung).
Ein Limiter dient zur Begrenzung von Signalpegeln ab einer definierten Grenze, sodass Übersteuerungen und Überlastungen verhindert werden können.
Verlustbehaftete Audiocodierung: Beispiel MP3
»Mp3s contain within them a whole philosophy of audition and a praxeology of listening. As a philosophy of audition, the mp3 makes use of the limitations of healthy human hearing. One might even say that the mp3 is a celebration of the limits of auditory perception.«
(Jonathan Sterne (2006): »The mp3 as cultural artefact«. In: new media & society, Vol. 8(5). S. 825-842.)
MP3 steht für MPEG-1 Audio Layer 3 und ist ein durch die Moving Pictures Experts Group formulierter Standard zur verlustbehafteten Codierung von Audio-Daten. Das Verfahren wurde seit Ende der 80er Jahre am Frauhnhofer-Institut für Integrierte Schaltungen (Erlangen) entwickelt. Formuliertes Ziel der Codierung ist es, bei massiv reduzierter Datenrate (s. Faustformel oben: etwa Faktor 10) unter Alltagsbedingungen einen Höreindruck zu erzeugen, der von unkomprimierten Audiodaten nicht bzw. kaum zu unterscheiden ist.
MP3 ist sicher das bisher wirkmächtigste Audiokompressionsverfahren und steht darüber hinaus auch in seinem technischen Aufbau beispielhaft für konkurrierende Codierungen.
MP3 Encoding
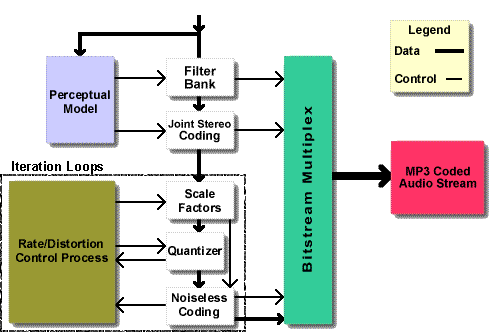
Die Encoding-Seite ist durch den MPEG Standard weniger genau spezifiziert als die Decoding-Seite. Dies führt dazu, dass unterschiedliche Encodierer zu durchaus unterschiedlichen Ergebnissen führen. Es lassen sich allerdings 5 Schritte nennen, die allen Encodern zugrunde liegen:
1. Das Signal wird durch eine Filterbank in einzeln prozessierte Frequenzbänder unterteilt.
2. Das ursprünglich serielle PCM Signal wird blockweise in den Frequenzbereich überführt (FFT).
3. Die beiden Stereo-Kanäle werden pro Block abgeglichen und je nach Einstellung (Mono, Stereo, Joint-Stereo, Dual-Channel) gespeichert.
4. Die Quantisierung der einzelnen Frequenzbänder ist für den größten Anteil der Datenreduktion (und damit der Verlustbehaftung) verantwortlich. Hier kommt ein psychoakustisches Modell (s.u.) zum Einsatz, um den Frequenzbändern Skalenfaktoren zuzuteilen, nach denen sie neu quantisiert werden. Kleinere Skalenfaktoren entsprechen einer feineren Quantisierung.
5. Eine (verlustfreie) Huffman-Codierung eliminiert Redundanzen aus dem Datenstrom; die MP3-Datenstruktur kombiniert Header und Frames.
Psychoakustisches Modell
Das psychoakustische Modell, das die MP3-Codierung zugrunde legt, nutzt die Eigenschaften des (gesunden) menschlichen Hörens, um »unnötige« Signalanteile zu erkennen und durch deren Einsparung die Datenrate zu reduzieren. ›Psychoakustisch‹ meint dabei die gesamte Körperlichkeit des eigentlichen Hörvorgangs:
»Psychoacoustic effects are based on the fact that the body creates sound by organizing vibration.« (Sterne 2006, 834)
Die MP3-Codierung nutzt dabei v.a. die folgenden Wahrnehmungseffekte aus:
1. Maskierungseffekte, d.h. Maskierung leiserer Frequenzanteile durch benachbarte lautere Frequenzanteile.
2. Zeitliche Maskierungseffekte, d.h. Maskierung von leiserer Anteile durch unmittelbar vorausgehende (oder sogar folgende) Töne.
3. Spatialisierung, d.h. die Erzeugung eines Raumeindrucks im Hören durch Stereophonie.

Um die Datenrate zu reduzieren, werden bei der MP3-Codierung, die einzelnen Frequenzbänder abhängig von der eingestellten zu erzielenden Rate nur so fein quantisiert, dass das resultierende Rauschen gerade nicht bzw. kaum wahrnehmbar wird (Maskierungseffekte). Außerdem werden wiederum je nach Einstellung des Encoders nicht zwei unabhängige Stereokanäle sondern ggf. nur ein Mono- plus ein Differenzsignal gespeichert (Spatialisierung).
Audio-Streaming
Als Audio-Streaming lassen sich zunächst alle über digitale Netzwerke übertragenen Audiodaten ohne finale Speicherung auf dem Endgerät zusammenfassen. Damit sind Online-Radio und kommerzielle, abonnementbasierte Streaming-Plattformen ebenso gemeint wie bspw. die Kommunikation zwischen Handy und Bluetooth-Lautsprecher.
Beim kommerziellen Streaming von Musik-Daten im Internet kommt meistens eine verlustbehaftete Codierung des Signals zum Einsatz (z.B. AAC (Apple Music), OGG (Spotify)), um die zur Übertragung benötigte Bandbreite zu reduzieren. Da die Codierungsverfahren sich unterscheiden, sagt hier die Datenrate alleine allerdings noch nicht unbedingt etwas über die resultierende Klangqualität aus. Ein Containerformat kombiniert ggf. Audio-, Video- und Meta-Daten. Für das eigentliche Streaming wird dann ein geeignetes Transport-Protokoll verwendet. Während Live-Streaming spezielle Protokolle erfordert (bspw. RTP, RTCP), reichen bei On-Demand-Streaming standardisierte Protokolle zur Dateiübertragung wie HTTP oder FTP.
Kulturinformatisch interessant an der immer weiteren Verbreitung von (kommerziellem) Musikstreaming ist auch die damit verbundene massenhafte Erhebung und Auswertung von Nutzungsdaten wie sie ähnlich in vielen weiteren Bereichen digitaler Kulturen zu beobachten ist (siehe Sitzung ›Big Data‹). Musiknutzung und -rezeption in digitalen Medien wird so auf eine neue Art und Weise beobachtbar. Gleichzeitig wird in diese Prozesse bspw. durch algorithmen-basierte Empfehlungen direkt eingegriffen. Klassische Formate der Musikdistribution werden nicht unbedingt obsolet, wandeln aber sicherlich ihre Gestalt (Bsp. Longplayer, Playlist, etc.).
Literatur
Henle, Hubert: Das Tonstudiohandbuch. Praktische Einführung in die professionelle Aufnahmetechnik. München 1998
Sterne, Jonathan: »The mp3 as cultural artefact«. In: new media & society, Vol. 8(5). 2016. S. 825-842.
Stotz, Dieter: Computergestützte Audio- und Videotechnik. Multimediatechnik in der Anwendung. Berlin 1995
