Phonographie
Phonographie (übersetzt: Klangschrift) meint das ›Mitschreiben‹ von Klängen als physikalische Ereignisse. Dafür wird die Luftdruckschwankung, die wir als Hörschall wahrnehmen, in ein anderes physikalisches Medium übertragen. Den einfachsten Fall stellt der 1877 von Thomas A. Edison erfundene Phonograph dar. Er wird über einen Aufnahmetrichter besprochen. Am Ende des Trichters ist eine Membran gespannt, daran ein Stichel angebracht. Dieser wird durch die eintreffenden Schallwellen in Schwingung versetzt. Vor dem Stichel sitzt ein mit Zinnfolie oder Wachs umkleideter Zylinder, der durch eine Handkurbel angetrieben wird. Wird der Zylinder bei aufgesetztem Stichel gedreht, schreibt der Phonograph die eintreffenden Schallwellen ›analog‹ in die Materialität der Walze ein. Die Wiedergabe funktioniert ganz entsprechend andersherum.
Digitalisierung
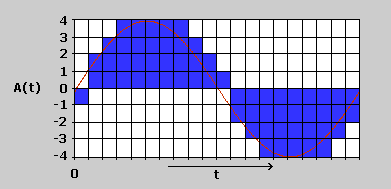
Analoge Audiosignale sind kontinuierliche Signale. Bei der Digitalisierung werden diese in eine regelmäßige Folge von diskreten Werten gewandelt. Hierzu wird die Amplitude des Signals in regelmäßigen Abständen abgetastet und den einzelnen Stichproben (=Samples) Werte aus einer begrenzten Wertemenge zugeordnet (Quantisierung). Dabei wird ein Raster verwendet, dass die möglichen Werte bestimmt. Die Abtastfrequenz (=Abtastrate, Abtastfrequenz, Samplefrequenz, Samplerate; in Hz oder kHz angegeben) bestimmt, wie oft das Signal pro Sekunde abgetastet wird. Die Auflösung (=Quantisierung; in bit angegeben) legt die mögliche Wertemenge pro Sample fest.
Die Digitalisierung von Audiodaten erfordert eine A/D- (und natürlich am Ende des Prozesses eine D/A) Wandlung. Die meisten Rechner verfügen bereits seit längerer Zeit über eingebaute und ins Betriebssystem integrierte Wandlerhardware. Der zur Zeit allgemein verfügbare ‚Standard‘ für die Audiohardware ist eine Digitalisierung in ‚Zeitscheiben‘ von 44,1 kHz und einer ‚Lautstärkerasterung‘ von 16 bit.
Jeder dieser Balken visualisiert einen diskreten Messwert (ein Sample in der technischen Definition). Die gezackte Begrenzungslinie entspricht in Annäherung dem kontinuierlichen Verlauf der Welle.
Dieses Verfahren heißt in der Fachsprache Pulse-Code-Modulation (PCM). In der Praxis wird statt der jeweiligen Abtastwerte oft nur die Differenz zur letzten Messung (Differential PCM), oder die Richtung des nächsten Werts (Delta-Modulation, 1-bit Wandlung) bestimmt, bevor zum Standard-Datenformat transformiert wird.
Datenübertragung und Speicherung
Für Audiodaten richtet sich nach den allgemeinen Möglichkeiten für Speicherung auf Festplatten, CD-ROMS, Wechselmedien etc. und Netzübertragung (Internet, LAN etc.). Dabei sind Hardware (Speicher- und Übertragungskapazität) und Software (Cacheorganisation und Protokolle) zu berücksichtigen. Sind Audiodaten erst einmal digitalisiert, unterscheiden sie sich um nichts von ihren Text- oder Bild-‚Kollegen‘.
Die Datenrate, die dabei pro Sekunde und Kanal anfällt, entspricht der Sampleauflösung mal der Samplefrequenz.
Beim üblichen Format (CD-Standard): Stereo, 44,1 kHz, 16 Bit ergeben sich:
2 (für 2 Stereokanäle) x 44100 x 16 = 1.411.200 Bit/s oder 176.400 Byte/s oder 172,26 KByte/s.
Übertragungsraten für andere Auflösungen und Samplefrequenzen (unkomprimiert):
| 44,1 kHz | 22 kHz | 11 kHz | |
| 16 Bit | 172 KByte/s | 88 KByte/s | 44 KByte/s |
| 12 Bit | 132 KByte/s | 66 KByte/s | 33 KByte/s |
| 8 Bit | 88 KByte/s | 44 KByte/s | 22 KByte/s |
Übertragungsraten (komprimiert):
Typische Performance Daten von MPEG-1 Layer III
| sound quality | bandwidth | mode | bitrate | reduction ratio |
| „telephone sound“ | 2.5 kHz | mono | 8 Kbps | 96:1 |
| „better than shortwave“ | 4.5 kHz | mono | 4.5 kHz | 48:1 |
| „better than AM radio“ | 7.5 kHz | mono | 32 Kbps | 24:1 |
| „similar to FM radio“ | 11 kHz | stereo | 56…64 Kbps | 26…24:1 |
| „near CD“ | 15 kHz | stereo | 96 Kbps | 16:1 |
| „CD“ | 15 kHz | stereo | 112..128 Kbps | 14..12:1 |
Faustregeln für den Bedarf an Speicherplatz:
Pro Minute werden bei unkomprimierten Daten (Stereo, 44,1 kHz, 16 bit) ca. 10 MByte Speicherplatz benötigt,
bei stark komprimierten Daten (Real Audio, MPEG-1/Layer 3) ca. 1 MByte.
bits und Bytes
1 Byte = 8 bit (ein halbes ‚Datenwort‘ von 16 bit);
1 kbit = 1000 bit
Die Präfixe Kilo (K) und Mega (M), die im Normalgebrauch den Faktor 1.000 bzw. 1.000.000 bezeichnen, werden im Bereich der bits und Bytes oft nach den 2er-Potenzen des binären Systems verwendet, also:
1 Kbit = 1024 bit = 128 Byte
1 Mbit = 1024×1024 bit = 1048576 bit = 131072 Byte = 128 KByte
Diese Praxis wurde allerdings offiziell seit 1996 geändert und folgende Benennung vorgeschlagen:
1 Kibibyte (KiB) = 1024 Byte, 1 Mebibyte (MiB) = 1024 · 1024 Byte.
Dennoch existieren zurzeit alle Verwendungen nebeneinander, so dass Verwirrungen möglich sind: Eine nach dem dezimalen 1 TByte angegebene Festplatte wird etwa vom Betriebssystem im binären Kontext mit 931 GByte erkannt.
Audiodatenformate
Unkomprimierte Formate:
.wav (MS-Windows-Format)
.aiff (audio interchange file format; auf Apple-Plattformen üblich)
.flac
Komprimierte Formate / Internet:
* MP3 (=MPEG 1; Layer 3) als gängigstes DRM-freies Dateiformat; Dateiendung .mp3
MP3 erlaubt als Kompressionscodec keine erweiterten Funktionen, selbst die bekannten ID3-Tags mit Angabe von Artist, Title etc. sind nur durch einen Trick möglich. Allerdings können die Dateien – wie jede andere Datei auch – mit einem Watermark (z.B. beim Kauf) ‚gestempelt‘ werden
* MP4 (=Container mit oder ohne DRM + meistens MP3 oder AAC codierten Daten) als neueres praktisches Containerformat mit hochwertig und effizient codierten Inhalten; Dateiendungen .mp4, .m4a (audio), .m4p (protected audio)
Beispiel: Audiodateien aus dem iTunes-Shop bestehen aus einem MP4 Container mit Apples DRM FairPlay und AAC codierten Inhalten
* WMA (=Microsofts proprietäres Audiokompressionsformat mit integrierter DRM Funktionalität); Dateiendungen .wma, .asf (advanced streaming format=streaming container für wma und anders codierte Daten)
WMA ist eng an das Windows-Betriebssystem gebunden, inzwischen erlauben jedoch auch Programme wie iTunes die Konvertierung von nicht DRM beschränkten WMAs in andere Formate
* AAC (Advanced Audio Coding) ist ein verbessertes MPEG 2 Verfahren.
Aussteuerung
Eine möglichst gute Aussteuerung des Aufnahmepegels ist die Voraussetzung für eine rauscharme und dynamikreiche A/D Wandlung. Anders als bei analogen Aufnahmeverfahren, für die diese Regel ebenfalls gilt, gibt es allerdings bei der Digitalisierung keinen Grenzbereich, sondern eine genau definierte obere Pegelgrenze, bei deren Überschreiten keine Abbildung der Wellenform mehr möglich ist. Es wird solange nur ein Wert (der Höchstwert) gemessen, wie der zulässige Pegel überschritten wird. Resultat ist eine ‚gekappte‘ Welle, die sich einer Rechteckschwingung annähert und mit dem Original kaum noch etwas gemeinsam hat.
Interferenz
Überlagerung zweier oder mehrerer Schwingungen mit dem Ergebnis von Interferenzschwingungen (Schwebungen)
Die Digitalisierung kontinuierlicher Phänomene wie Bilder und Töne ist prinzipiell mit einer Rasterung verbunden. Dabei können sich die Rasterfrequenz und eine wellenförmige Struktur des Gegenstands überlagern und weitere, vorher nicht existente Schwingungen ergeben. Interferenzprobleme bei der Digitalisierung treten aus zwei Ursachen auf:
– das zu digitalisierende Phänomen hat selbst eine ’natürliche‘ Wellenstruktur, wie etwa die Luftschwingungen des Schalls oder sich periodisch bewegende Gegenstände im Bewegtbild oder
– ein ’naturgemäß‘ unperiodisches Phänomen wurde durch Medientransformationen bereits gerastert.
Aliasing
Beim Digitalisieren können Frequenzen entstehen, die im Original nicht vorhanden sind. Diese Artefakte oder ‚Aliasfrequenzen‘ des Digitalisierungsvorgangs sind Ergebnisse einer unzureichenden Abtastfrequenz. Hier gilt – wie bei jedem Wellenphänomen – das Nyquist/Shannon-Theorem: Die Abtastrate muß mindestens das Doppelte der zu digitalisierenden Frequenz betragen.
Das Abtasttheorem (=Sampling Theorem, Shannon-Theorem, Nyquist/Shannon-Theorem) besagt, „daß ein bandbreitenbegrenztes Signal ohne Informationsverlust rekonstruiert werden kann, sofern die Abtastfrequenz mindestens doppelt so groß wie die maximale Signalfrequenz ist.“ (Zander, S. 705).
Enthält das abgetastete Signal Frequenzen, die über der halben Abtastfrequenz liegen, entstehen bei der AD-DA Umsetzung Frequenzen (Aliasfrequenzen, Spiegelfrequenzen), die im Originalsignal nicht enthalten waren. Um diesem als Aliasing bezeichneten Phänomen entgegenzuwirken, wird das Originalsignal vor der Abtastung durch einen Tiefpaßfilter in seiner Bandbreite begrenzt. Die Grenzfrequenz des Filters muß aufgrund begrenzter Flankensteilheit einen bestimmten Betrag unter der halben Abtastfrequenz liegen.
Da in Audiosignalen immer – ob gewünscht oder nicht – hochfrequente Anteile vorhanden sind, die jede Datenrate und Speicherkapazität sprengen würden, gibt es nur zwei Lösungswege für dieses Problem (i.d.R. kombiniert angewandt):
Filterung – im Audiosignal werden alle Frequenzen über der beabsichtigten halben Digitalisierungsfrequenz herausgefiltert. Es ist allerdings mit vertretbarem Aufwand nicht möglich, auf analogem Wege alle Frequenzen zu entfernen, sie werden lediglich gedämpft (‚Q-Faktor‘, ‚Dämpfungsfaktor‘, ‚Flankensteilheit‘ des Filters).
Oversampling – das Signal wird mit einem Vielfachen (z.B. 64fach) der Abtastfrequenz abgetastet, um Aliasing zu vermeiden. Auf digitalem Weg werden dann die hohen Frequenzen herausgerechnet. Oft wird die Kombination beider Verfahren angewendet.
Die folgenden Beispiele zeigen die Verteilung der einzelnen Messpunkte in Abhängigkeit von der Freqenz der zu digitalisierenden Schwingung. Die Samplingfrequenz (=zeitliche Abtastrate) beträgt bei allen Beispielen 44100 Hz:
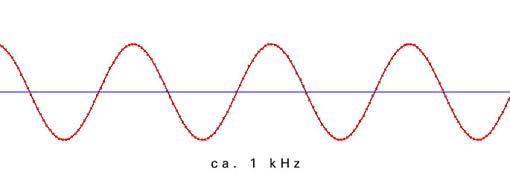
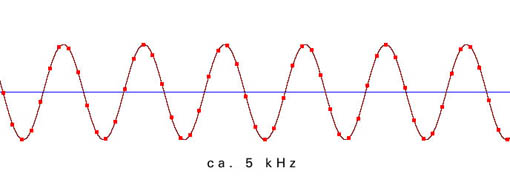
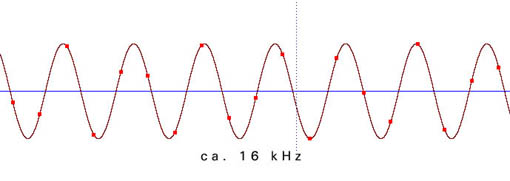
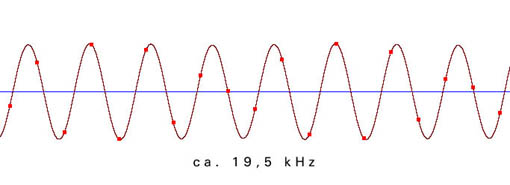
Aus der ungenauen Abtastung in der Nähe der Grenzfrequenz ergibt sich ein phasenungenaues und amplitudenverändertes Signal:
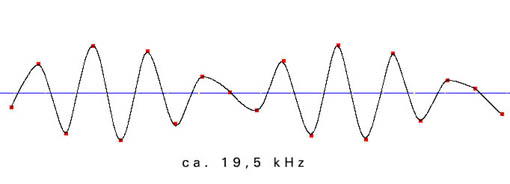
Dynamik – Signal/ Rauschabstand
Die Dynamik eines Signals bezeichnet den Umfang seiner Lautstärkeunterschiede oder einfacher gesagt, sie bestimmt, wie weit sich ein Pianissimo und ein Fortissimo unterscheiden. Um die Nuancen eines Konzerts für Violine und Orchester wiederzugeben, ist eine wesentlich größere Dynamik erforderlich als etwa für eine Nachrichtensendung. Manchmal ist eine große Dynamik sogar unerwünscht, etwa in Werbeclips, die sich durch einen gleichbleibend hohen Pegel aus dem Programmumfeld herausheben sollen.Gemäß den Eigenschaften des menschlichen Gehörs wird die Dynamik in der logarithmischen Einheit Dezibel angegeben.
Der Dynamikumfang natürlicher Instrumente:
| Sprache | Sologesang | Streicher | Klavier | Orchester |
| 15-20 dB | 40-50 dB | 30-35 dB | 40-50 dB | 30-70 dB |
Um die Dynamik des Originalsignals beizubehalten, muß der Signal/Rauschabstand der Dynamik des Originalsignals mindestens entsprechen. Bei elektrischen und elektronischen Übertragungssystemen wird die technisch mögliche Dynamik als Systemdynamik bezeichnet. Sie ist als Differenz von Übersteuerungsgrenze und Rauschpegel definiert.
Systemdynamik von analogen Übertragungssystemen:
| Studioverstärker | Plattenspieler | Compakt Cassette | MW-Radio | Muzak Tape |
| 100 dB | 50 dB | 40 dB | 30 dB | 20 dB |
Die maximale Systemdynamik errechnet sich nach der Formel:
S(ignal)/N(oise) [dB] = 6,02n + 1,76
n entspricht der Länge der Binärzahl in Bit. Bei einer Auflösung von 16 Bit beträgt die maximale Systemdynamik demnach ca. 98 dB. Die tatsächlich nutzbare Dynamik und somit der effektive Signal/Rauschabstand liegt allerdings weit darunter, da ein bewerteter Störpegel von 14 dB, ein Schutzabstand zum Störpegel von 20 dB (Footroom) und eine Aussteuerungsreserve von 10 dB (Headroom) berücksichtigt werden müssen. Bei einer 16-Bit-Auflösung ergibt sich somit ein effektiver Signal/Rauschabstand von 54 dB. Dynamik [dB] = 98 – 14 – 20 -10 = 54
Spitzfindigkeiten mit dB (Dezibel)
Dezibel ist eine dimensionslose Größe (wie z.B. Prozent) auf einer logarithmischen Skala. Sie wird u.a. für Pegel verwendet, weil das Gehör auf Pegelveränderungen nicht linear reagiert.
Es gelten folgende Faustregeln:
Spannungsbezogener Pegel
Studionormpegel bei 0 dB (in Europa 0,7746 V)
Höchstpegel bei + 6 dB
Verdopplung des Pegels = X + 6 dB
(und umgekehrt: Halbierung X – 6 dB, deshalb steht im Soundeditor auch die 50 % Marke bei – 6 dB)
Verdoppelung der Lautstärkeempfindung (falls das überhaupt festzustellen ist) ungefähr bei X + 10 dB
Schalldruckbezogener Pegel
Setzt man die Hörschwelle bei 0 dB ( 2 · 10 hoch-5 Pa) an, liegt die Schmerzschwelle etwa bei 120-130 dB.
Bewertete Schallpegelangaben wie dB(A) folgen den Eigenschaften des Gehörs, das tiefe und hohe Frequenzen leiser als mittlere Frequenzen wahrnimmt.
Cut, Copy and Paste
Cut: Ausschneiden eines ausgewählten Bereichs in die Zwischenablage
Copy: Kopieren eines ausgewählten Bereich in die Zwischenablage
Paste: Einfügen der Daten aus der Zwischenablage
Trim/Crop: Freistellen des ausgewählten Bereichs
Es sollte darauf geachtet werden, immer in den Nulldurchgängen oder Pegelspitzen mit gleichem Pegel zu schneiden, so daß keine unbeabsichtigten Rechteckflanken entstehen, die sich als „Knackser“ bemerkbar machen.
Durch Wiederholen eines bestimmten Segments (oder auch des gesamten Materials) entsteht ein Loop. Dieser kann dazu benutzt werden, die quasistationäre Phase eines Klanges zu verlängern oder um eine ständige Rhythmusspur (Drumloop) zu erzeugen.
Dämpfung/Verstärkung/Normalisierung/Gleichspannungsanteil
Durch diese Funktionen kann der Pegel des Audiosignals bestimmt werden. Hierbei werden immer alle Werte des Signals in gleichem Maße verändert. Als Verstärkung wird allgemein die Pegelveränderung bezeichnet, also dessen Anhebung und Absenkung, als Dämpfung wird die Absenkung des Pegels bezeichnet. Als Normalisierung bezeichnet man eine gleichmäßige Pegelanhebung des Signals. Durch eine vorherige Analyse wird der Zeitpunkt mit dem höchsten Pegel (Peak) bestimmt. Nun wird das Signal derart verstärkt, daß der Peak die eingestellte Aussteuerungsgrenze (maximal 0 db) erreicht. Der Gleichspannungsanteil (DC-Offset) wird oftmals im gleichen Arbeitsschritt entfernt.
Addition/Mischung
Die Mischung von Audiodateien kann durch die Addition der einzelnen Samplewerte erreicht werden. Auch ohne die Funktionalität digitaler Mehrspurrecorder und digitaler Mischpulte können dadurch Mischungen meherer Audiodateien erzeugt werden.
Hüllkurven
Durch Hüllkurven können komplexe Pegelveränderungen grafisch editierbar auf das zu bearbeitende Signal angewendet werden. Die klassische ADSR-Hüllkurve der analogen Klangsysnthese kann dabei simuliert werden. Es lassen sich jedoch auch sehr komplexe Hüllkurven mit fast beliebig vielen Segmenten erstellen.
Fades
Durch Fades sind gleichmäßige Ein- und Ausblendungen des Signals möglich. Man verwendet je nach Einsatzzweck linare oder logarithmische Fades. Für Überblendungen (Crossfades) werden Fades mit einem logarithmischen Verlauf verwendet, da dadurch die empfundene Lautstärke des Summensignals weitgehend gleich bleibt.
Quantisierungsfehler
Da das wertkontinuierliche Analogsignal bei der Digitalisierung auf Werte einer endlichen Wertemenge abgebildet wird, kommt es zu Rundungsfehlern. Da diese Fehlerbeträge im Zeitverlauf statistisch gleich verteilt auftreten, können sie als Rauschen interpretiert werden (Quantisierungsrauschen). Insbesondere bei Signalen, die in einem geradzahligen Verhältnis zur Abtastfrequenz stehen, ergibt sich ein unangenehmes ‚tonales‘ Rauschen, da die Fehlerrate nicht mehr zufällig ist, sondern dem Phasenverhalten des Signals folgt.

Dithering
Um den signalabhängigen Klangcharakter des Quantisierungsrauschens bei geringer Aussteuerung des abzutastenden Signals zu unterdrücken, wird dem Originalsignal vor der Digitalisierung eine geringe Rauschspannung (Dither-Rauschen) beigemischt. Auch bei der Requantisierung auf digitaler Ebene wird ein Dithersignal zugesetzt, um die dabei entstehenden Fehler zu maskieren.
Sample-Editoren / Wave-Editoren
dienen zur Bearbeitung von Audiodat(ei)en. (s.u.)
Sequenzer
waren zunächst reine MIDI-Anwendungen (Sequenz=Tonfolge), entwickelten sich jedoch in den 1990er Jahren zu universellen und hochkomplexen Werkzeugen der digitalen Musikproduktion. Sie integrieren MIDI- und Audio-Daten in einem gemeinsamen Arrangement und übernehmen die zeitliche Synchronisation beider Datentypen. Darüberhinaus stellen sie die wichtigsten Bearbeitungsmöglichkeiten bis hin zur Einbindung von Effekten und Steuerparametern für Klangerzeuger zur Verfügung.
Übungs-Input: Audio-Editing in Ableton Live
![]()
Audacity (kostenloser Wave-Editor)
Ocenaudio (kostenloser Wave-Editor)
